【超入門】二進法とは?十進法との違いが一気にわかるやさしい解説
「二進法とは?」
と聞かれると、正直ちょっと身構えていませんか。
0と1だけで数を表すと聞くと、
「難しそう」
「自分には関係なさそう」
と感じる人も多いと思います。
でも実は、二進法とはスマホやパソコン、ゲーム機など、私たちの身近なデジタル機器を動かすために欠かせない、とてもシンプルな仕組みなんです。
なぜ人間は10進法を使い、機械は二進法を使うのか。
その違いを知らないままだと、デジタルの話がずっとモヤモヤしたままかもしれません。
この記事では、二進法とは何かをゼロからやさしく整理し、「なるほど、そういうことか」とスッと理解できるように解説します。
苦手意識がある人こそ、ぜひ読み進めてみてください。
- 二進法とは0と1の数え方
- 位は1・2・4…と増える
- 二進法→十進法は足し算
- 十進法→二進法は割り算
- 機械は二進法が得意な理由
位(1の位・10の位・100の位)など「いつもの数え方」を確認すると、二進法の理解がスッと進みます。
二進法とは何かを初心者向けにやさしく理解しよう

二進法とは、「0と1だけで数を表す方法」のことです。
一見むずかしそうに感じますが、考え方はとてもシンプルで、実は私たちが毎日使っているスマホやパソコンの中で当たり前に使われています。
ここでは、二進法とは何か、なぜ必要なのかを、10進法との違いを意識しながら、初めての方にもわかるように整理していきます。
二進法とはどんな数の表し方なのか
二進法とは、「使える数字が0と1だけ」の数え方です。
10進法が「0〜9」を使うのに対して、二進法は「0と1」だけ。
そのかわり、桁(けた)が増えるスピードが違うので、見た目がちょっと長くなります。
- 10進法:指で「0〜9」まで数えられる(数字がたくさん)
- 二進法:スイッチみたいに「OFF(0) / ON(1)」だけで数える
| 項目 | 10進法 | 二進法 |
|---|---|---|
| 使う数字 | 0〜9 | 0と1 |
| 1つ桁が増えるタイミング | 10になったら | 2になったら |
| 得意な世界 | 人間の日常 | コンピュータ・電子機器 |
使う数字が0と1だけになる理由
コンピュータの中は、ざっくり言うと電気のスイッチで動いています。
スイッチは「入ってる / 入ってない」がいちばんわかりやすいですよね。
だから二進法は、0(OFF)と1(ON)の2つだけにすると、とても安全で間違いにくいんです。
- もし「0〜9」みたいに10段階で電気を区別しようとすると、ちょっとしたブレでズレやすい
- でも「OFF/ON」なら、多少ブレてもどっちかにハッキリ決めやすい
「0〜9の10種類の旗の色」を遠くから見分けるより、
「白か黒か」を見分けるほうが、ずっとカンタン…みたいな感じです。
0と1だけなら、回路(電気の道)を「ONにする/OFFにする」だけでよくて、設計がシンプルになりやすいです。
たくさんの段階を判定するより、「0か1か」の判定のほうが、動作が速くて迷いが少ないです。
電気にはどうしてもノイズ(ゆらぎ)があるので、2択のほうが「誤判定」を減らしやすいです。
「0と1だけで足りるの?」って思うかもですが、組み合わせればOKです。
たとえば、10進法は「10になったら桁が増える」ですが、二進法は「2になったら桁が増える」だけ。
ルールがシンプルだから、コンピュータが得意なんです。
- 二進法:0 → 1 → 10 → 11 → 100 → 101 …
- ポイント:「2になったら繰り上がり」と覚えるだけでOK
二進法とは、機械が安全に・速く・間違いにくく数を扱うために、0と1だけで数を作る方法です。
二進法とは何のために生まれた仕組みなのか
二進法とは、人間のためというより、機械が間違えずに数を扱うために生まれた考え方です。
人間と機械では、数の「得意・不得意」がまったく違います。
その違いをうまく埋めるために考えられたのが、二進法という仕組みです。
私たち人間は、生まれたときから10進法に慣れています。
指が10本あるので、「0〜9」を使う数え方は直感的で、とても分かりやすいですよね。
- 指で数えられる
- 見た目で大小が分かりやすい
- 暗算や感覚的な判断がしやすい
つまり、10進法は人間向けにとても優しい数の仕組みなんです。
一方で、機械(コンピュータ)は指も感覚もありません。
あるのは電気の流れだけです。
- 電気が流れている
- 電気が流れていない
この2つの状態しか区別できない世界で、
「0〜9までを正確に判断しろ」と言うのは、かなり無理があります。
人間と機械で数の扱い方が違う理由
人間は「だいたい」「感覚」で判断できますが、
機械ははっきり決まっていないと動けません。
| 比べるポイント | 人間 | 機械(コンピュータ) |
|---|---|---|
| 数の判断 | 感覚・経験でOK | 決まった条件が必要 |
| あいまいさ | 許される | 許されない |
| 得意な数 | 10進法 | 二進法 |
機械にとっては、0か1かの二択がいちばん安心です。
その安心な仕組みを人間側が理解しやすい形にしたものが、
「二進法」という考え方だと考えられます。
二進法とは、人間と機械の「数の考え方のズレ」を埋めるために生まれた仕組みです。
二進法とは十進法と何が一番違うのか
二進法と十進法のいちばん大きな違いは、「使える数字の数」と「繰り上がりのルール」です。
十進法は「0〜9」で数えて、10になったら次の位へ。
二進法は「0と1」で数えて、2になったら次の位へ。
この違いがわかると、二進法が一気にラクになります。
10進法は「10個たまったら箱を1つ増やす」世界。
二進法は「2個たまったら箱を1つ増やす」世界。
箱=位(けた)だと思えば、イメージしやすいです。
- 数字の種類:10進法は10個、二進法は2個
- 繰り上がり:10進法は「10」、二進法は「2」で起きる
- 見た目:二進法は同じ数でも桁が長くなりやすい
使う数字の数の違いを比べてみよう
十進法は10種類の数字(0〜9)を使います。
二進法は2種類の数字(0と1)しか使いません。
たったこれだけの違いが、桁の増え方や見た目の長さにつながります。
| 項目 | 十進法 | 二進法 |
|---|---|---|
| 使える数字 | 0,1,2,3,4,5,6,7,8,9 | 0,1 |
| 同じ数を表すときの見た目 | 短くなりやすい | 長くなりやすい |
| 感覚のわかりやすさ | 人間にとって直感的 | ルールで理解するとラク |
十進法は、道具箱に10種類の道具が入っている感じ。
二進法は、道具が2種類しかないけど、組み合わせで何でも作る感じ。
道具が少ないぶん、作るときは「並べ方(ルール)」が大事になります。
位が増えるルールの違いをイメージで理解
位(けた)が増えるタイミングは、その進法の「次の数」になったときです。
十進法なら「10」、二進法なら「2」で繰り上がります。
ここを押さえると、二進法の並びが“暗号”に見えなくなります。
| 十進法(ふつうの数) | 二進法(0と1だけ) | ここがポイント |
|---|---|---|
| 0 | 0 | スタート |
| 1 | 1 | ここまでは同じ |
| 2 | 10 | 二進法は2で繰り上がる |
| 3 | 11 | 「10の次」 |
| 4 | 100 | また繰り上がって桁が増える |
十進法は「9の次が10」で桁が増える。
二進法は「1の次が10」で桁が増える。
つまり、二進法の“1”は、十進法の“9”みたいな役目だと思うと理解しやすいです。
位(けた)は「何個たまったら次の位へ行くか」のルールで決まります。
十進法は10個たまると次へ。二進法は2個たまると次へ。
この違いだけで、二進法の見た目が長くなる理由も説明できます。
二進法は桁が増えやすいぶん、機械にとってはルールが単純で扱いやすいんです。
(この「扱いやすさ」は、次の「変換」や「計算」の章でさらにスッキリします。)
二進法とは十進法と比べて、使う数字の数が少なく、繰り上がりが早いのが最大の違いです。 このルールさえ押さえれば、二進法は「暗号」ではなく「ただの数え方」に見えてきます。
二進法とは日常生活ではどう関わっているのか
二進法とは、ふだんの生活で自分が意識して使う数え方ではありません。
でも実は、私たちは毎日、二進法に支えられた世界で生活しています。
この章では「どこで・どう関わっているのか」を、身近な例だけで見ていきます。
スマホ、パソコン、ゲーム機、テレビ、電子レンジ…。
これらはすべて中身がコンピュータで動いています。
そして、そのコンピュータの中で数を扱うときに使われているのが二進法です。
私たちは画面で「100円」「18時」「75%」のような10進法の数字を見ています。
でもその裏側では、コンピュータがそれらを二進法に変換して処理しています。
- 人間:100(十進法)
- 機械:1100100(二進法)
- 結果:また人間向けに100として表示
つまり、変換は全部コンピュータが自動でやってくれているんです。
コンピュータやデジタル機器との関係
コンピュータの中では、文字も写真も音も、ぜんぶ0と1の組み合わせとして扱われています。
二進法は、デジタル機器が世界を理解するための共通語のようなものです。
- 写真:明るさや色を0と1で記録
- 音楽:音の波を細かく分けて0と1で保存
- 文字:文字コードとして0と1に変換
- 動画:大量の画像を0と1で高速処理
どれも見た目はカラフルですが、中身は白黒(0と1)です。
コンピュータの中には、ものすごい数の小さなスイッチがあります。
そのスイッチが「入っているか/切れているか」の組み合わせで、
私たちが見ている画面や音が作られていると考えると、二進法の存在が自然に感じられます。
私たちは二進法を計算しなくてもスマホを使えます。
それは、二進法が裏方として完璧に働いているからです。
ただ、仕組みを知ると「なぜこんな動きができるのか」が見えてきます。
二進法とは、私たちが意識しないところでデジタル生活を支えている数の仕組みです。
見えないけれど、スマホもネットも、すべて二進法の上に成り立っています。
二進法は学校でいつ習う内容なのか
二進法は、小学校では基本的に学びません。
中学校〜高校で、「情報」や「数学の考え方」を理解する流れの中で登場します。
ここでは「なぜ小学校では出てこないのか」「どんな場面で学ぶのか」を整理します。
学校の算数・数学は、理解しやすい順番で進みます。
まずは日常生活と直結した10進法をしっかり身につけてから、「考え方としての数」を学ぶ段階で、二進法が登場します。
小学校では扱わない理由
小学校の算数は、「数に慣れること」がいちばん大切です。
そのため、生活の中で使う10進法が中心になります。
- 指で数えられない
- 生活の中で使う場面が少ない
- 「なぜ必要?」が伝えにくい
二進法は仕組みとしてはシンプルですが、
日常と結びつけにくいため、最初の学習には向いていません。
まずは「数=身近なもの」という感覚を育てることが先。
そのため、小学校では10進法に集中する構成になっています。
中学・高校で出てくる場面
中学〜高校になると、「数の仕組みそのもの」を考える学習が始まります。
その流れで、二進法が登場します。
| 学校段階 | 出てくる教科・場面 | 学ぶ目的 |
|---|---|---|
| 中学校 | 情報・技術分野 | コンピュータの仕組みを知る |
| 高校 | 情報Ⅰ・数学的な考え方 | 論理的に数を扱う力を育てる |
この時期になると、「仕組み」や「ルール」を理解する力が育ってきます。
だからこそ、「10進法が当たり前じゃない」という考え方を学ぶ意味が出てくるのです。
二進法は、小学校では扱わず、中学〜高校で「考え方」として学ぶ内容です。
数を「使う」段階から、「仕組みを理解する」段階に進んだときに登場します。
二進法とはどのように計算や変換で使われるのか

二進法とは仕組みを知るだけでなく、「どうやって数を表すのか」「どうやって計算や変換をするのか」を知ることで、一気に理解が深まります。
.0この章では、二進法の位の考え方や、10進法との変換方法を中心に、数字を追いかけながら、二進法の使い方をやさしく見ていきます。
二進法の「位」の考え方をやさしく整理
二進法の「位」は、1、2、4、8、16…と2倍ずつ増えるのが特徴です。
そして各位には「0か1」しか入らないので、
必要な位を1にして足し算するだけで、どんな数でも作れます。
10進法だと、位は「1、10、100、1000…」ですよね。
二進法はそれが「1、2、4、8、16…」になるだけ。
つまり、“位の並びが違うだけで、ルール自体は似てる”と考えるとラクです。
10進法は「1円・10円・100円…」みたいな箱がある感じ。
二進法は「1円・2円・4円・8円…」の箱が並んでる感じです。
そして各箱に入れられるのは0枚か1枚だけ。
だから、必要な箱だけ「1枚入れる(=1)」で数が作れます。
1の位・2の位・4の位の基本イメージ
二進法の位は、右から順にこう並びます。
1の位 → 2の位 → 4の位 → 8の位…
ここではまず、最初の3つ(1・2・4)だけを使って感覚をつかみます。
| 位(右から) | 名前 | 重み(価値) | 入る数字 |
|---|---|---|---|
| 1つ目 | 1の位 | 1 | 0 or 1 |
| 2つ目 | 2の位 | 2 | 0 or 1 |
| 3つ目 | 4の位 | 4 | 0 or 1 |
作り方はシンプルで、1にした位の「重み」を足すだけです。
たとえば、(4の位・2の位・1の位)が1・0・1なら…
4 + 0 + 1 = 5 という感じ。
| 二進法(4 2 1の位) | 足し算 | 十進法 |
|---|---|---|
| 000 | 0+0+0 | 0 |
| 001 | 0+0+1 | 1 |
| 010 | 0+2+0 | 2 |
| 011 | 0+2+1 | 3 |
| 100 | 4+0+0 | 4 |
| 101 | 4+0+1 | 5 |
| 110 | 4+2+0 | 6 |
| 111 | 4+2+1 | 7 |
ここまで見えると、「二進法=暗号」じゃなくて、ただの足し算に見えてきません?🙂
このパートでは、まず「位=重み(1/2/4…)」の感覚をつかむことを優先しているので、
まだ「割り算で変換する方法」や「大きい桁(8/16/32…)」は深掘りしていません。
そこは後続の見出しで、同じテンションでちゃんとつなげます。
二進法の位は、右から1・2・4・8…と2倍で増えます。
各位に入るのは0か1だけなので、1になっている位の重みを足すだけで十進法に直せます。
二進法で数を数えるとどうなるのか
二進法の「位」や「重み」は分かってきたけど、
「じゃあ実際に数を数えたら、どう並ぶの?」と思いますよね。
ここでは、二進法で1ずつ数を増やすと何が起きるのかを、目で追える形で確認します。
二進法でも、やっていることは「1を足す」だけ。
ただし、使える数字が0と1だけなので、
1の次は「2」ではなく、桁が増えるのがポイントです。
| 十進法 | 二進法 | イメージ |
|---|---|---|
| 0 | 0 | 何もONじゃない |
| 1 | 1 | 1の位がON |
| 2 | 10 | 2の位がON |
| 3 | 11 | 2と1がON |
| 4 | 100 | 4の位だけON |
| 5 | 101 | 4と1がON |
| 6 | 110 | 4と2がON |
| 7 | 111 | 全部ON |
「111」の次に来るのが「1000」になるのが、二進法らしさです。
二進法で8や29を表す考え方
二進法で数を表すときは、使えそうな一番大きい位から順に見ていきます。
その位が使えたら1、使えなければ0にするだけです。
8は「8の位」がぴったり使えます。
なので、8の位を1、それより小さい位は全部0。
29は少し大きいですが、やることは同じです。
- 16(使える → 1)
- 8(使える → 1)
- 4(使える → 1)
- 2(使えない → 0)
- 1(使える → 1)
ここでは「位を見て足し引きする」直感的な方法を使っています。
割り算を使う正式な変換手順もありますが、理解の第一歩としてはこの考え方で十分です。
二進法で数を数えると、0と1の組み合わせで桁がどんどん増えていきます。
大きな数でも、使える位を1にしていくだけで表せます。
二進法を十進法に直す基本的な考え方
二進法を十進法に直すと聞くと、「計算がむずかしそう…」と感じがちですが、実はやっていることは小学生でもできる足し算だけです。
- 右から順に「1・2・4・8…」の位を見る
- その位が「1」なら足す
- 「0」なら足さない
つまり、1になっている位だけを拾って足すという考え方です。
一つずつ足して確認する方法
どんな二進法の数でも、同じ手順で確認できます。
ここでは例を使って、一つずつ足す流れを見てみましょう。
| 位 | 重み | 0 or 1 | 足す? |
|---|---|---|---|
| 1の位 | 1 | 1 | 足す → +1 |
| 2の位 | 2 | 1 | 足す → +2 |
| 4の位 | 4 | 0 | 足さない |
| 8の位 | 8 | 1 | 足す → +8 |
- 左から見てしまう → 必ず右から
- 0の位も足してしまう → 0は無視
- 暗算しようとする → 紙に書けばOK
この方法は「考え方を理解する」ことを目的にしています。
試験や実務では、もっと速い変換方法が使われることもありますが、基礎としてはこの足し算方式がいちばん確実です。
二進法を十進法に直すときは、1になっている位だけを足す。
難しい計算はなく、仕組みが分かれば誰でも確認できます。
十進法を二進法に変換するシンプルな方法
十進法(ふつうの数)を二進法に直す方法はいくつかありますが、初心者が一番ラクなのは、割り算と余りだけで進める方法です。
理屈がまだ完全じゃなくても、手順通りにやれば必ず答えにたどり着けるので安心してね🙂
- 数を2で割る
- 出た余り(0か1)を書いていく
- 割った結果をまた2で割る…を繰り返す
- 最後に、余りを下から上へ読む
割り算を使った変換の流れ
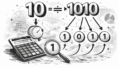
ここでは例として、13(十進法)を二進法にしてみます。
「2で割る → 余りを書く」を繰り返すだけです。
| 割る前の数 | ÷2 の商 | 余り(0/1) | メモ |
|---|---|---|---|
| 13 | 6 | 1 | 13は奇数→余り1 |
| 6 | 3 | 0 | 6は偶数→余り0 |
| 3 | 1 | 1 | 3は奇数→余り1 |
| 1 | 0 | 1 | ここで終了(商が0) |
余りは上から順に 1 → 0 → 1 → 1 と出ました。
でも答えは、その逆。下から上へ読むので…
余りは、実は右端(1の位)から順に決まっていく情報なんです。
だから、最初に出た余りが「一番右の数字」になり、最後に出た余りが「一番左の数字」になります。
なので、結果として下から読むのが正解になります。
- 余りを上から読んでしまう(逆に読む!)
- 商が0になっても続けてしまう(0になったら終了)
- 余りが2以上になると思い込む(2で割るので余りは0か1だけ)
十進法を二進法に変換するシンプルな方法は、2で割り続けて余りを集めるやり方。
余りは下から上へ読むのがコツで、手順通りにやれば必ず変換できます。
二進法の考え方が分かってきたら、次は実際に「10進法から2進法」へ変換してみる番です。 整数・小数・1Byte表記まで、つまずきやすいところをまとめて練習できます。
二進法の計算はなぜ機械に向いているのか
二進法が機械に向いている理由は、とてもシンプルです。
「0か1か」だけを判断すればいいから。
人間にとっては味気なく見えるこの仕組みが、機械にとっては最高にやさしいのです。
人間は「7+8=15」みたいに、頭の中で考えて判断できます。
でも機械は、自分で考えたり、あいまいな判断をするのが苦手です。
だからこそ、答えがハッキリ決まる仕組みが必要になります。
二進法の0と1は、「ON / OFF」「通る / 通らない」「ある / ない」と同じ感覚です。
これなら、機械でも迷わず判断できます。
コンピュータが二進法を使う理由
コンピュータの中は、基本的に電気で動いています。
電気は「流れている」「流れていない」の2状態がいちばん安定します。
これをそのまま0と1に当てはめたのが二進法です。
二進法の足し算は、
0+0、0+1、1+0、1+1の4パターンだけ。
これなら、機械でも超高速で処理できます。
| 項目 | 十進法 | 二進法 |
|---|---|---|
| 使う数字 | 0〜9 | 0と1だけ |
| 計算パターン | かなり多い | とても少ない |
| 誤作動のリスク | 高くなりがち | 低い |
0か1か、はっきりしているので、ノイズ(電気のゆらぎ)があっても判断しやすいのが二進法。
これが、コンピュータが安定して動く大きな理由の一つです。
二進法は、0と1だけという単純さのおかげで、機械が速く・正確に・安定して計算できる仕組みです。だからこそ、コンピュータの世界では二進法が選ばれ続けています。
二進法とは何かを振り返って全体を整理【まとめ】
二進法とは、最初はとっつきにくく感じがちですが、仕組みを一つずつ見ていくと、とても素直で単純な数の考え方だと分かってきます。
最後に、この記事で押さえたポイントをまとめて整理しましょう。
- 使う数字は0と1だけ
- 位は1・2・4・8…と2倍ずつ増える
- 1になっている位の重みを足すだけで数が決まる
特別な暗号ではなく、ルールが少ない数え方だと考えると理解しやすいです。
- 二進法 → 十進法:1の位を足し算
- 十進法 → 二進法:2で割って余りを見る
- どちらも難しい計算は不要
「向きが違うだけで、考え方はシンプル」という点が大事です。
- 機械は0か1かの判断が得意
- 計算ルールが少なく、速くて安定
- 電気のON/OFFと相性がいい
二進法とは、人間よりも機械の都合に合わせた数の仕組みだと言えます。
二進法とは、「知らないと使えない知識」ではありません。
でも知っていると、コンピュータやデジタルの世界が急に分かりやすくなる考え方です。
ここまで理解できたなら、二進法はもう「怖い存在」ではありません 🙂
二進法とは、0と1だけで数を表す、とても合理的な仕組み。
人間には10進法、機械には二進法。
それぞれに合った数え方がある、という理解でOKです。



コメント